河南省应用数学中心（河南大学）成员杨翔宇与合作者在非凸优化算法研究中取得重要进展, 提出了一种求解非凸Lp-范数球欧式空间投影的高效算法。相关成果以“Towards an Efficient Approach for the Nonconvex Lp-ball Projection: Algorithm and Analysis”为题在理论机器学习领域的顶级学术期刊 Journal of Machine Learning Research (JMLR) 上在线发表。

在现代机器学习和信号处理等领域， 探索系统解的稀疏性已经成为基本且重要的研究任务之一。一般地，稀疏解通常可以提高系统的鲁棒性、增强模型的可解释性、改善模型的泛化性以及降低模型的推理成本。为了系统地促进模型解的稀疏性，机器学习模型通常会包含稀疏正则函数。其中，非凸Lp-范数正则函数的有效性已被诸多工作证实，从而受到了优化与机器学习社区研究者们的广泛关注。特别地，针对欧式空间中的非凸Lp-范数球投影问题，杨翔宇与合作者展开了深入地研究并取得了重要的成果。

在研究过程中，研究人员发现在大规模优化问题中，计算Lp-范数球投影的高效数值算法十分有限。另一方面，Lp-范数的非凸、非光滑以及非利普希茨数学性质对算法的分析与设计提出了巨大挑战。为此，研究团队首先推导出表征该问题最优解的一阶必要条件，继而设计了一种迭代重加权L1-范数球投影 (Iteratively Reweighted L1 Ball Projection, IRBP) 算法计算原问题一阶驻点的数值方法。该算法实现简单, 且计算效率高 (参见图1和图2)。此外，研究团队证明了所提算法的全局收敛性以及收敛速率。该算法的提出为求解一类难以处理的稀疏约束优化问题提供了坚实的研究基础。

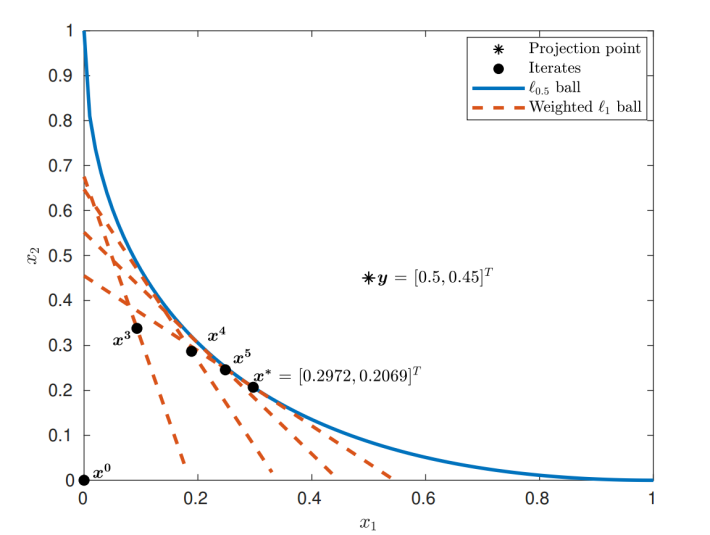
图1. IRBP求解二维L0.5范数球投影问题产生的迭代序列路径

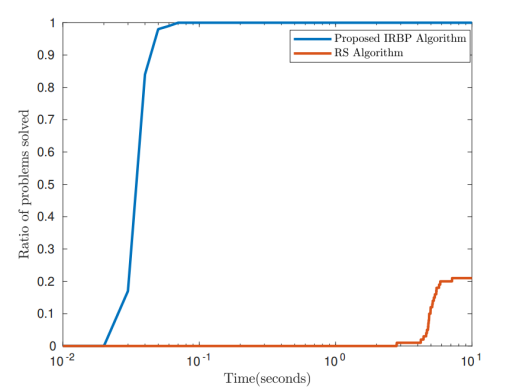
                               (a) p = 0.4                               

(b) p = 0.8

图2. IRBP与当前先进算法的性能比较

此项研究由河南省应用数学中心（河南大学）、上海科技大学以及华盛顿大学单位协作完成。中心成员杨翔宇为第一作者。

据悉，JMLR由麻省理工学院出版社（MIT Press）出版，依托于麻省理工学院的计算机科学与人工智能实验室（MIT CSAIL: MIT Computer Science & Artificial Intelligence Lab），旨在刊登人工智能与机器学习领域的高质量前沿研究成果，是国际上公认的计算机领域顶级期刊之一，同时也是中国计算机学会 (CCF) 推荐的 A类国际学术期刊，2022年影响因子3.654. JMLR旨在刊登机器学习领域的高质量学术研究, 其对论文的研究动机、理论证明、实验结果及论文写作等各个方面都要求极高，审稿过程极为严格。国内一流科研单位每年能在JMLR上独立发表的论文数量极少。

文章链接：https://www.jmlr.org/papers/volume23/21-0133/21-0133.pdf