河南省应用数学中心（河南大学）葛志昊教授和陈玉祥硕士研究生在热多孔弹性模型数值计算方面取得了重要进展，相关成果以“Multiphysics Finite element method for quasi-static thermo-poroelasticity”为题在计算数学权威期刊Journal of Scientific Computing(JSC)在线发表文章，链接：https://link.springer.com/article/10.1007/s10915-022-01877-w。

      热多孔弹性力学模型是热-流体-固体相互作用的偏微分方程组，在二氧化碳封存，地热能提取等领域有重要应用（见图1），由于其具有数值不稳定性（见图2和图3）、强耦合性和非线性等特点，求其解析解极其困难，因此发展稳定的数值离散方法对于指导实际工程实践意义重大。

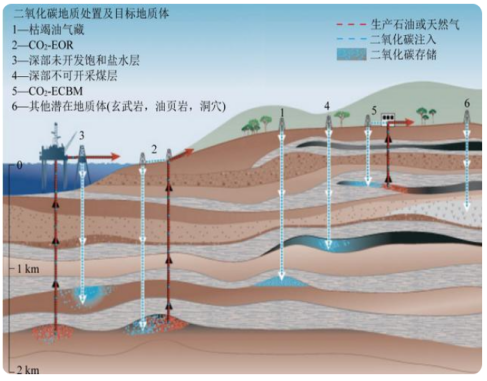
图1 碳捕集、利用与封存技术示意图

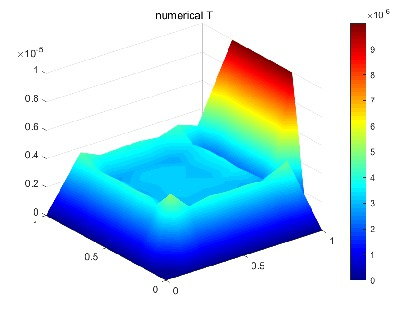
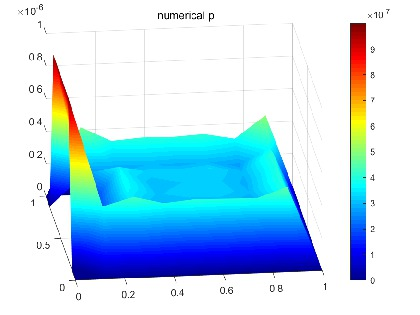
图2 采用P2-P1-P1元求解原模型温度出现数值振荡          图3 采用P2-P1-P1元求解原模型压力出现数值振荡

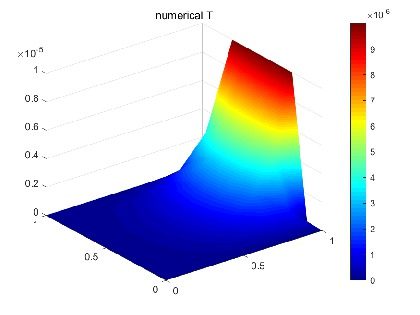
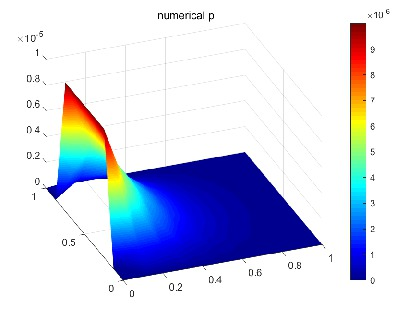
图4 采用P2-P1-P1-P1元求解重构后的模型温度没有数值振荡现       图5采用P2-P1-P1-P1元求解重构后的模型压力没有数值振荡现象

     在该论文中葛志昊教授和陈玉祥同学提出了稳定的多物理有限元方法。为了克服闭锁现象以及揭示形变, 扩散和传热的多物理过程, 该论文将原模型重构为一个流体耦合问题，证明了弱解的适定性, 给出了所设计的全离散多物理场有限元方法的最优阶误差估计，数值算例验证了方法的有效性（见图4和图5）。