黄琼敖博士在计算数学权威期刊Journal of Scientific Computing发表重要研究成果

河南大学数学与统计学院、河南省应用数学中心(河南大学)成员黄琼敖博士在退化Cahn-Hilliard方程保结构格式的构造方面取得重要进展，相关成果以“A structure-preserving, upwind-SAV scheme for the degenerate Cahn-Hilliard equation with applications to simulating surface diffusion”为题在计算数学权威期刊Journal of Scientific Computing (JSC)在线发表。

Cahn-Hilliard方程在材料科学、流体力学、图像修复等领域具有重要的作用。理论分析表明，耦合退化mobility和对数Flory-Huggins势能的Cahn-Hilliard方程在足够低温时的尖锐界面极限(sharp-interface limit)是表面扩散(surface diffusion)。长久以来，人们殷切希望能够通过数值模拟的方法验证这一结果。然而，由于mobility的退化性以及对数势的奇异性，导致构造出同时满足能量耗散、质量守恒和相变量有界的保结构格式颇为困难。在该论文中黄琼敖博士和合作者将迎风格式的思想首次应用于SAV方法，为退化Cahn-Hilliard方程构造出了一个高效的保结构格式，同时借助于维数分裂技术，将高维问题的求解解耦成若干一维问题，从而节省了大量的计算消耗。最后，通过数值模拟的方法验证了上述理论结果(见图1和图2)。

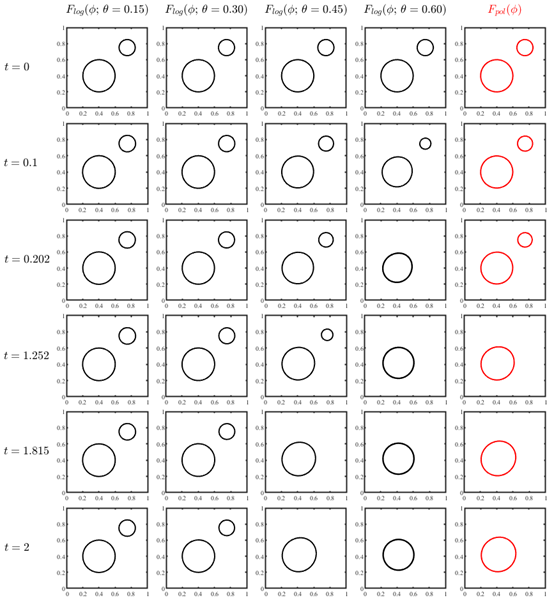
图1 大圆和小圆在不同势能下的演化图

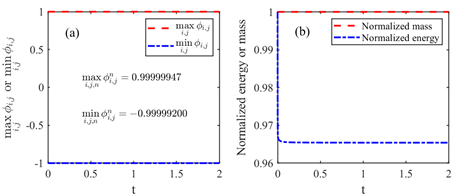
图2 对数Flory-Huggins势能下的相变量最值、能量和质量的演化图

此项研究成果由河南大学数学与统计学院、河南省应用数学中心(河南大学)以及武汉大学合作完成。中心成员黄琼敖博士为第一作者，武汉大学袁成博士为通讯作者、蒋维副教授和杨志坚教授为重要合作者。

文章链接：https://link.springer.com/article/10.1007/s10915-023-02380-6